SYMPHONIE is an ocean model developed by the SIROCCO system group (CNRS & Toulouse University).
Model description:
The 3-D ocean circulation model SYMPHONIE (Marsaleix et al., 2008, 2019) is based on the Navier-Stokes primitive equations solved on an Arakawa curvilinear C-grid under the hydrostatic and Boussinesq approximations. The model makes use of an energy conserving finite difference method described by Marsaleix et al. (2008), a forward-backward time stepping scheme, a Jacobian pressure gradient scheme (Marsaleix et al., 2009), the equation of state of Jackett et al. (2006), and the K-epsilon turbulence scheme with the implementation described in Costa et al (2017). Horizontal advection and diffusion of tracers are computed using the QUICKEST scheme (Leonard, 1979) and vertical advection using a centered scheme. Horizontal advection and diffusion of momentum are each computed with a fourth order centered biharmonic scheme as in Damien et al (2017). The biharmonic viscosity of momentum is calculated according to a Smagorinsky-like formulation derived from Griffies and Hallberg (2000). The lateral open boundary conditions, based on radiation conditions combined with nudging conditions, are described in Marsaleix et al. (2006) and Toublanc et al. (2018).
Vertical grid
The VQS (vanishing quasi-sigma) vertical coordinate described in Estournel et al, (2021) is used to avoid an excess of vertical levels in very shallow areas while maintaining an accurate description of the bathymetry and reducing the truncation errors associated with the sigma coordinate (Siddorn et al, 2013).
Horizontal grid
The standard horizontal bipolar grid (where the poles are separated by 180 degrees of latitude) is adapted to our coastal problem by tilting the axis of the poles in order to place one of the 2 poles in the continental part near the coastal zone of interest where the resolution is increased (Estournel et al, 2012). In To Duy et al. (2022), the nearest pole is located in the centre of the Vietnamese peninsula so that the resolution is maximum (1km x 1km) over most of the coastline (including the upwelling region studied) and decreases almost linearly seaward, the resolution at the open boundary being about 4.5km x 4.5km.
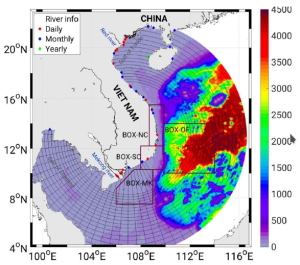
Rivers
At the mouth of the river, the river boundary current is consistent with the discharge of the river as in Reffray et al (2004), while the vertical shape of the current is given by a gradient condition allowing the current to adjust by itself to the dynamics of the river plume in front of the mouth (rather than arbitrarily prescribing a possibly inappropriate vertical profile). The boundary condition is applied in two steps (Nguyen-Duy et al, 2021). Step 1 is given by the above-mentioned gradient condition, leading to a provisional solution of the current, while Step 2 ensures that the total flow is consistent with the expected discharge from the river.
Tides
The implementation of the tide, described in Pairaud et al (2008, 2010), consists on the one hand of the amplitude and phase of the tide introduced at the open lateral boundaries and on the other hand of the astronomical plus loading and self-attraction potentials. As in Pairaud et al (2008, 2010), the 9 main harmonics of the tide are considered, the forcing fields being provided by the 2014 release of the FES global tidal model (Lyard et al, 2006). On the continental shelves, the turbulence generated by the friction of the tidal currents on the bottom is generally significant. Near the bottom the temperature and salinity stratification is in principle homogenised over a layer that can be up to several tens of metres high depending on the strength of the tide. CMEMS fields provide boundary conditions for temperature, salinity, surface elevation and currents associated with non-tidal processes. Because the tide is not taken into account in the CMEMS simulation, the stratification is insufficiently mixed near the bottom.
As the errors induced on T and S are potentially important, we make a modification to the CMEMS T,S fields before introducing them at the open boundaries of our model (Nguyen-Duy et al, 2021). This modification consists in homogenising T and S near the bottom, over a thickness deduced from the expected theoretical height of the tidally induced turbulent bottom layer. This height is estimated from the friction velocity associated with the tidal current, i.e. *D = 0. 1u /f (Csanady, 1982) where f is the Coriolis parameter and the friction velocity, u* , is calculated from the tidal harmonics of the depth-averaged current provided by FES, and a drag coefficient of 1e-3.
Short waves and swell
Recently, the model equations have evolved to be adapted to non-hydrostatic phase-resolved wave modelling (Marsaleix et al, 2019). In practice, the equations are derived from the method presented by Lee et al 2006 which offers a reasonable compromise between the computational cost and the accuracy required to correctly describe wave propagation in shallow water.
Alongside this major development, new lateral boundary conditions have been specially developed, as well as parameterisations to introduce wave breaking and the effect of rocky bottoms on wave dissipation.
References
Csanady, 1982 – Circulation in the Coastal Ocean – 281 pages
Costa A., Doglioli A. M., Marsaleix P., Petrenko A. A., 2017. Comparison of in situ microstructure measurements to different turbulence closure schemes in a 3-D numerical ocean circulation model. Ocean Modelling. https://doi.org/10.1016/j.ocemod.2017.10.002
Damien, P., Bosse, A., Testor, P., Marsaleix, P. and Estournel, C. (2017), Modeling postconvective submesoscale coherent vortices in the northwestern Mediterranean Sea. J. Geophys. Res.
Oceans. doi:10.1002/2016JC012114. http://dx.doi.org/10.1002/2016JC012114
Estournel, C., E. Bosc, M. Bocquet, C. Ulses, P. Marsaleix, V. Winiarek, I. Osvath, C. Nguyen, T. Duhaut, F. Lyard, H. Michaud, and F. Auclair, 2012. Assessment of the amount of Cesium-137 released into the Pacific Ocean after the Fukushima accident and analysis of its dispersion in Japanese coastal waters. 117, C11014, Journal of Geophysical Research, 117, C11014, doi:10.1029/2012JC007933
Estournel C., Marsaleix P., Ulses C., 2021. A new assessment of the circulation of Atlantic and Intermediate Waters in the Eastern Mediterranean, Progress in Oceanography, https://doi.org/10.1016/j.pocean.2021.102673 Griffies, S., and R. Hallberg (2000), Biharmonic friction with a Smagorinsky-like viscosity for use in large-scale eddy-permitting ocean models, Mon. Weather Rev., 128(8), 2935–2946, doi:10.1175/1520-0493(2000)128 < 2935:BFWASL>2.0.CO;2.
Jackett, D.R., McDougall, T.J., Feistel, R., Wright, D.G., Griffies, S.M., 2006. Algorithms for density, potential temperature, conservative temperature, and the freezing temperature of seawater. J. Atmos. Ocean. Technol. 23, 1709–1728.
Lee, J.W., Teubner, M.D., Nixon, J.B., Gill, P.M., 2006. Application of the artificial compressibility method for turbulent open channel flows. Int. J. Numer. Methods Fluids 51, 617–633.
Leonard B.P., 1979. A stable and accurate convective modeliing proceure based on quadratic upstream interpolation. Computer methods in applied mechanics and engineering 19, 59-98
Lyard, F., Lefevre, F., Letellier, T., Francis, O., 2006. Modelling the global ocean tides: modern insights from Fes2004. Ocean Dynamics 56, 394–415.
Marsaleix P., Auclair F., Estournel C., 2006, Considerations on Open Boundary Conditions for Regional and Coastal Ocean Models. Journal of Atmospheric and Oceanic Technology, 23,1604-1613, http://dx.doi.org/10.1175/JTECH1930.1
Marsaleix P., Auclair F., Floor J. W., Herrmann M. J., Estournel C., Pairaud I., Ulses C., Energy conservation issues in sigma-coordinate free-surface ocean models. Ocean Modelling. 20, 61-89. http://dx.doi.org/10.1016/j.ocemod.2007.07.005
Marsaleix P., Auclair F., Estournel C., 2009. Low-order pressure gradient schemes in sigma coordinate models: The seamount test revisited. Ocean Modelling, 30, 169-177. http://dx.doi.org/10.1016/j.ocemod.2009.06.011
Marsaleix, P., Michaud, H., Estournel, C., 2019. 3D phase-resolved wave modelling with a non-hydrostatic ocean circulation model. Ocean Modelling, 136, 28-50. https://doi.org/10.1016/j.ocemod.2019.02.002
Michaud H., Marsaleix P., Leredde Y., Estournel C., Bourrin F., Lyard F., Mayet C., Ardhuin F., 2012. Three-dimensional modelling of wave-induced current from the surf zone to the inner shelf. Ocean Science, 8, 657-681, http://dx.doi.org/10.5194/os-8-657-2012
Nguyen-Duy Tung, Ayoub Nadia K., Marsaleix Patrick, Toublanc Florence, De Mey-Frémaux Pierre, Piton Violaine, Herrmann Marine, Duhaut Thomas, Tran Manh Cuong, Ngo-Duc Thanh, 2021. Variability of the Red River Plume in the Gulf of Tonkin as Revealed by Numerical Modeling and Clustering Analysis, Frontiers in Marine Science, https://www.frontiersin.org/article/10.3389/fmars.2021.772139
Pairaud I. L., Lyard F., Auclair F., Letellier T., Marsaleix P., 2008, Dynamics of the semi-diurnal and quarter-diurnal internal tides in the Bay of Biscay. Part 1: Barotropic tides, Continental Shelf Research, 28, 1294-1315 http://10.1016/j.csr.2008.03.004
Pairaud I. L., Auclair F., Marsaleix P., Lyard F., Pichon A., 2010. Dynamics of the semi-diurnal and quarter-diurnal internal tides in the Bay of Biscay. Part 2: Baroclinic tides, Continental Shelf Research, 30, 253-269, http://dx.doi.org/10.1016/j.csr.2009.10.008
Siddorn J.R., Furner R., 2013. An analytical stretching function that combines the best attributes of geopotential and terrain-following vertical coordinates. Ocean Modelling 66, 1–13
To Duy, T., Herrmann, M., Estournel, C., Marsaleix, P., Duhaut, T., Bui Hong, L., and Trinh Bich, N.: The role of wind, mesoscale dynamics, and coastal circulation in the interannual variability of the South Vietnam Upwelling, South China Sea – answers from a high-resolution ocean model, Ocean Sci., 18, 1131–1161,
https://doi.org/10.5194/os-18-1131-2022, 2022
Toublanc F., N.K. Ayoub, F. Lyard, P. Marsaleix, D.J. Allain, Tidal downscaling from the open ocean to the coast: a new approach applied to the Bay of Biscay, Ocean Modelling, Volume 124, April 2018, Pages 16-32, ISSN 1463-5003, https://doi.org/10.1016/j.ocemod.2018.02.001.
Yinglong J. Zhang, Eli Ateljevich, Hao-Cheng Yu, Chin H. Wu, Jason C.S. Yu, 2015. A new vertical coordinate system for a 3D unstructured-grid model, Ocean Modelling, 85, 16-31.
Examples of simulations done with SYMPHONIE




